摘要
摘要:关键类是理解软件的起点。准确地识别软件中的关键类对于简化软件理解工作具有重要意义。尽管已有很多关键类识别方面的工作,但是存在以下三点不足:1)软件网络不够准确,忽视了很多交互关系;2)度量类重要性的指标忽视了软件的重要结构特征(如类之间的非接触依赖、不同依赖的强度差异等);3)现有工作集中于无监督方法,有监督方法相对匮乏。针对上述问题,提出了一种基于加权有向网络指标集的关键类预测方法:首先,提出“加权有向的类依赖网络CCNWD”抽象软件在类粒度的结构;其次,提出加权网络指标集WDNM刻画CCNWD边上的权值对类重要性的影响;最后,分别用无权有向网络度量集(NM)、设计度量集(DM)、NM+DM、WDNM+DM作为特征集,并经过SMOTUNED类不平衡处理后输入到随机森林模型中构建关键类预测模型。6个开源Java软件上的数据实验表明,相较于基于NM构建的关键类预测模型,基于WDNM构建的关键类预测模型,本文的模型取得了更好的AUC值。与此同时,DM+NM和DM+WDNM上构建的关键类预测模型相较于DM上构建的关键类预测模型,AUC值提高了8%以上。
软件网络
“软件网络”(Software Network)是一种将软件系统结构抽象为复杂网络 的建模方式,通常用于分析类、模块或组件之间的依赖关系和交互模式。其核心思想是:
- 节点(Nodes) :
代表软件中的基本单元,如类 (Class)、函数、模块等。- 例如,在面向对象的Java项目中,每个类可能是一个节点。
- 边(Edges) :
表示节点之间的依赖关系 或交互关系 。- 例如:
如果类A调用了类B的方法,则从A到B有一条有向边。
如果类C依赖于类D的某个属性,则可能用边的权重表示依赖强度。
- 例如:
- 网络类型 :
无权网络 (Unweighted Network):仅表示是否存在依赖关系(边存在与否)。
加权网络 (Weighted Network):边的权重反映依赖的强度(例如方法调用次数、依赖的属性数量等)。
有向网络 (Directed Network):边有方向,体现依赖的单向性(如A依赖B,但B不依赖A)。
“加权有向的类依赖网络CCNWD”
原缺点与作者提出的“加权有向的类依赖网络CCNWD”,做出的优化。
首先,文中提到的软件网络 特指对软件中类与类之间依赖关系的抽象,但现有方法存在以下问题:
- 未考虑权重 :传统方法(如无权有向网络NM)仅记录类之间是否有依赖,忽视了不同依赖的强度差异 (例如频繁调用和偶尔调用的区别)。
- 遗漏非接触依赖 :某些隐式的间接依赖关系(如通过接口或继承形成的依赖)未被建模。
- 结构特征缺失 :未捕捉关键结构模式(如高扇出/扇入、中心性等),导致关键类识别不准确。
- 关键结构模式(如高扇出/扇入、中心性等)
- 1. 高扇出和高扇入:
- 想象一下一个社交圈子里的朋友网络。
- 高扇出:就像一个特别活跃的人,他认识很多朋友,每次分享信息时,很多人会收到他的消息。这个人“发出”的信息很多。用图中的话,就是他有很多“出线”连接。
- 高扇入:相反,有一些非常受欢迎的人,很多人都会给他发信息或关注他,他“收到”的信息很多。这就是“扇入”很多。
- 2. 中心性:
- 想象一下一个学校的领导者或者老师。
- 中心性高的节点(人)在网络中像是“中心点”,连接很多人,信息可以很快传到很多地方。这就像是班级里的班长,无论谁需要帮助,都能找到他或她。
- 总结:
- 高扇出的人喜欢传递信息,发出很多消息。
- 高扇入的人收到很多信息,可能很重要或很受欢迎。
- 中心性高的人在网络中扮演着“枢纽”的角色,连接很多人,信息传递很快。
- 关键结构模式(如高扇出/扇入、中心性等)
其次,改进后的“CCNWD”网络:
作者提出的加权有向类依赖网络 (Class Dependency Network with Weight and Direction, CCNWD)针对上述问题进行了优化:
- 加权 :每条边的权重量化依赖强度(例如方法调用频率、参数传递数量等)。
- 有向 :明确依赖方向(如A调用B,边方向为A→B)。
- 更全面的依赖类型 :包含直接调用、继承、接口实现等非接触依赖关系。
WDNM
WDNM (Weighted Directed Network Metrics )是文中提出的加权有向网络指标集 ,用于量化类在加权有向类依赖网络 (CCNWD)中的重要性。其核心目标是通过结合边的权重 (依赖强度)和方向 (依赖关系的单向性),更精确地捕捉类在软件网络中的关键角色。
WDNM与传统无权网络指标(NM)的区别
| 指标类型 | NM(无权网络) | WDNM(加权网络) |
| 边的处理 | 仅表示存在/不存在依赖(0/1) | 量化依赖强度(如调用频率、参数数量等) |
| 方向性 | 有向单无权重 | 有向且有权重 |
| 核心关注点 | 结构连接性 | 依赖强度与结构共同作用 |
| 示例 | 入度(In-Degree) | 加权入度(Weighted In-Degree) |
WDNM的作用
- 捕捉依赖强度差异 :
例如,类A调用类B 100次(权重高)与调用1次(权重低),WDNM能区分二者对类B重要性的影响,而传统NM无法体现。 - 建模非接触依赖 :
通过继承、接口实现等形成的间接依赖被赋予权重,避免遗漏关键类的隐式影响。 - 提升预测模型性能 :
实验表明,使用WDNM作为特征集(结合设计度量DM)构建的随机森林模型,在AUC指标上优于基于NM的模型。
应用示例
假设在Java项目中:
类UserService调用了类DatabaseUtil的5个方法,且每次调用传递3个参数(权重=5×3=15)。
类Logger仅被调用1次(权重=1)。
WDNM会为UserService分配更高的加权出度(15),而NM仅记录其出度为1(存在调用关系)。因此,WDNM能更准确地识别UserService作为关键类。
DM、NM、WDNM三者的对比表格:
| 维度 | DM | NM | WDNM |
| 方向性 | 无方向性 | 有向性 | 有向性 |
| 权重信息 | 无权重 | 无权重 | 有权重 |
| 依赖建模 | 无依赖关系 | 显式依赖(存在与否) | 显式依赖 + 权重 + 非接触依赖 |
| 典型指标 | CBO、WMC、DIT | 入度、出度、PageRank | 加权入度、加权介数中心性 |
| 适用场景 | 传统代码质量评估 | 网络结构分析 | 高精度关键类识别 |
0 引言
概要一
软件在其生命周期内需要不断更新以适应不断新增的用户需求。
成功的面向对象软件通常会包含大量的类,但实现核心功能的是极少数类,这些类被称为“关键类”。
复杂网络理论引入软件工程领域,将软件的内部结构抽象成网络模型——“软件网络”,其中节点代表类,边代表类之间的依赖关系,并从复杂软件网络的视角开展了大量的关键类识别方面的研究,取得了较好的效果。
现有的关键类识别工作大致可分为两类:基于无监督学习的关键类识别方法和基于有监督学习的关键类预测方法
概要二
现有的研究还存在着以下不足:
- 现有工作主要集中于无监督方法,有监督的关键类预测方法相对匮乏;
- 现有的基于有监督学习的关键类预测方法依赖的软件网络不够准确,忽视了类之间很多重要的交互关系及交互关系的强度,导致所构建的度量指标集不能准确刻画软件的结构特征,进而影响了基于这些指标构建的模型的性能。
针对上述问题,本文提出了一种基于加权有向网络指标集的关键类预测方法KCP-WN (Key Class Prediction based on Weighted directed Network metrics),预测软件中的关键类。
概要三
包含如下步骤:
- 首先,提出“加权有向的类依赖网络”(Weighted Directed Class Coupling Network, CCNWD)模型抽象软件的结构;
- 其次,提出加权网络指标集 (Weighted Directed Network Metrics, WDNM) 刻画软件网络的权值及边的方向对类重要性的影响;
- 最后,分别用无权有向网络度量集 (Network Metrics, NM)、软件设计度量集 (Design Metrics, DM)、NM+DM、WDNM+DM作为特征,并经过SMOTUNED类不平衡处理后输入到随机森林模型中构建关键类预测模型,实现关键类的预测。
1 相关研究
现有的关键类识别工作大致可分为两类:基于无监督学习的关键类识别方法和基于有监督学习的关键类预测方法
无监督学习的关键类识别方法:
在类标签信息未知的情况下,通过对软件网络拓扑结构的度量来量化节点的重要性,进而识别软件中的关键类。
有监督学习的关键类预测方法:
在构建(或引入)新的软件度量指标集,并以这些指标为特征训练机器学习模型,构建关键类预测模型。
该文章:
本文的工作属于基于有监督学习的关键类预测方法。但是不同于现有的工作,本文引入了加权有向软件网络模型,并构建了相应的度量指标集(即WDNM),有助于解决现有工作的不足,从而提高关键类预测模型的性能。
2 KCP-WN方法
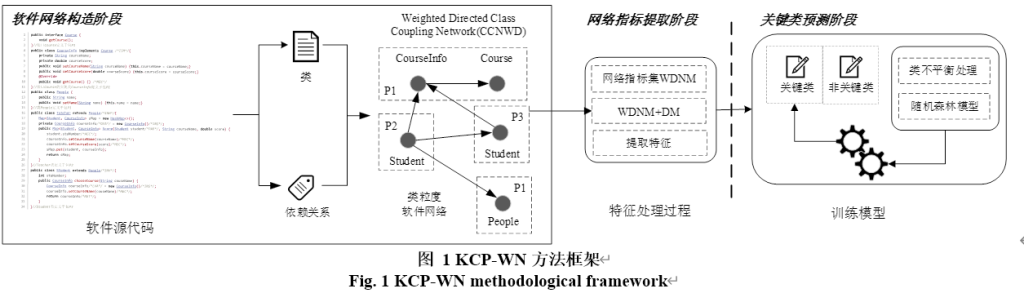
本文提出的KCP-WN方法的框架如图 1所示
KCP-WN包含三个阶段:软件网络的构造、网络度量指标的提取以及关键类预测模型的训练。
- 首先,通过解析Java项目的源代码抽取软件结构信息,并将其进一步表示成CCNWD。
- 其次,基于CCNWD构建加权有向网络度量指标集WDNM。
- 最后,分别将WDNM以及WDNM与软件设计度量DM的混合结果(WDNM+DM)作为特征,经由样本类不平衡处理后入输入到随机森林模型进行训练,从而实现关键类的预测。
2.1 软件网络的构造
DM 指标分为两类:
- 规模度量(Size)
- 反映类的内部复杂度,如属性数量、方法数量等。
- 依赖度量(Coupling)
- 衡量类与其他类的交互强度,分为“导出依赖”(Export)和“导入依赖”(Import)。
NM:
- 其核心思想是通过分析类依赖网络的连通性和中心性特征,识别潜在的关键类。
- NM 的特点是不考虑依赖强度 (即仅记录依赖关系是否存在,边权为 0 或 1),但保留了依赖方向性(如 A→B 表示 A 依赖 B)。
AUC值:
AUC(Area Under the Curve) 是机器学习中用于评估二分类模型性能的重要指标,尤其在类别分布不平衡的场景下表现尤为突出。它衡量的是接收者操作特性曲线(ROC曲线)下的面积 ,通过综合考虑模型的真阳性率(TPR)和假阳性率(FPR),反映模型对正负样本的整体区分能力。AUC是评估二分类模型鲁棒性的核心指标,尤其适用于类别不平衡的场景(如软件工程中的关键类识别)。
实验结果表明,在DM+NM上构建的关键类预测模型比DM上构建的预测模型具有更好的AUC值。
在这项工作中,NM的计算是基于他们所构建的无权有向软件网络,该网络包括了软件内部三种类型的依赖关系:泛化、实现和依赖(由于聚合、组合和依赖关系是语义级别,无法在源代码层面进行细致的区分,因此将这三种关系归为一类并统称为“依赖”)。
但仅考虑了类节点之间的部分依赖关系,忽视了依赖的强度。
类依赖强度实际上反映的是依赖关系的复杂程度以及类之间交互的紧密程度,刻画的是系统内部类与类之间的相互作用。
因此,仅考虑依赖方向而忽略了依赖强度的软件网络无法准确地描绘软件的内部结构。为了更准确地表示软件内部结构,本文进一步考虑了类依赖强度。
网络CCNWD
本文进一步考虑了类依赖强度。我们使用自主研发的软件网络分析平台SNAP,构建加权有向的类粒度软件网络CCNWD,其定义如下:
定义1:对于OO程序P,将其抽象成加权有向的类依赖软件网络,即CCNWD =(V, L, W)。其中,V节点集,表示P中的类(或接口)集合;L是有向边集,表示依赖关系的集合。
通常,类之间的依赖关系有九种类型,即局部变量(LVA)、全局变量(GVA)、继承(INH)、接口实现(IIM)、参数类型(PAR)、返回类型(RET)、实例化(INS)、字段访问(ACC)和方法调用(MEC)。
若两个类之间存在以上一种或多种依赖,则会存在一条有向边从依赖请求方指向依赖服务方。W是边上的权重集合。
如何定义和计算边的权重呢?目前的研究中,有些工作将依赖次数累加作为类节点之间的边权。这种赋权方法的问题在于:将所有依赖类型视为相同,不能准确反映类之间依赖关系强度的差异。实际上,从软件之间的交互关系来看,不同依赖类型在软件系统中的重要性各不相同,其依赖强度也应有所区别。
为了打破这种传统软件网络赋权的局限性,本文采用基于依赖分布的加权方式DWM(Distribution-based Weighting Mechanism)。DWM通过跟踪依赖关系在包内和包间的位置来量化依赖强度。
DWM的具体计算方法如下:
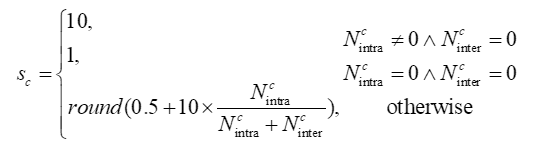
其中,Ncintra和Ncinter分别表示依赖关系 c 分布在同一个软件包内和不同软件包的次数。函数round()是对计算数值进行四舍五入运算,并保留整数。
本文对上述九种耦合类型的依赖强度进行量化,并将量化结果作为软件网络的权重。具体而言,某种关系出现的次数与该种关系权重的积作为由于该种关系产生的边权值。若两个类之间存在多种关系,则将他们的累加和作为边的最终权值。
2.2 加权指标集的提取
网络度量反映并揭示了网络结构与功能方面的规律。
将7种指标分别应用在CCNWD上,并进一步考虑链路权重,从而提出了加权的网络度量套件WDNM (Weighted Directed Network Metrics)。
- BaryC-W
- BETW-W
- CLOSE-W
- EIGEN-W
- HITS-W(包含Hub和Authority)
- PageRank-W
2.3 关键类预测模型的训练
在将网络度量指标以及对应的软件类标签输入至机器学习模型中训练的过程中,为了尽量避免数据划分的随机性所导致的评估性能的偏差,本文采用十次三折交叉验证。其中,一次交叉验证的算法流程图如图 2所示。交叉验证作为机器学习中常用的模型评估技术,其核心思想是将原始数据集划分为k个大小近似相等的子集(亦称“折”)。在每次验证过程中,选取其中一个子集作为测试集,剩余的k-1个子集则构成训练集,用于模型的训练。此过程重复k次,每次轮换测试集,以确保每个子集均有机会被用于模型性能的评估。通过计算k次测试结果的平均值,有效减少了单次数据划分的偶然性影响,提高了模型泛化能力的评估精度。特别地,本文进行十次独立的三折交叉验证,进一步增强了评估结果的可靠性。然而,由于软件中关键类与非关键类的数量存在着明显的差异,导致训练集中类别比例不平衡,因此在将其输入到随机森林模型训练前,需对样本进行类不平衡处理。
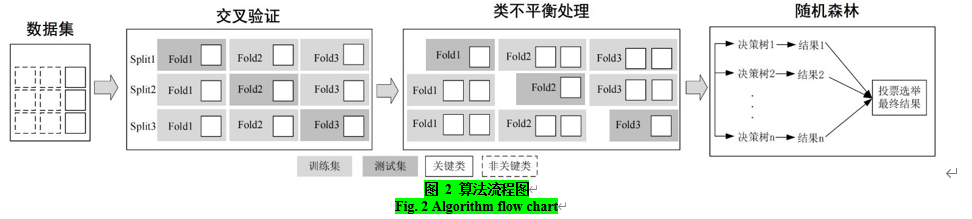
2.3.1 类不平衡处理
相关文献表明,尽管软件内有成百上千的类,但关键类数量仅为20-30个。因此在软件中存在着严重的类不平衡问题:即非关键类远多于关键类。类不平衡会导致分类模型在训练过程中更倾向于非关键类,忽略关键类,从而降低对关键类的预测性能。为解决这一问题,本文使用SMOTUNED(Autotuning Version of SMOTE)算法,该算法属于过采样算法。SMOTUNED作为SMOTE的改进算法,与后者最大的区别在于是否需要手工设置参数:SMOTE算法是基于欧式距离对样本进行线性插值生成新样本。而SMOTUNED则是在SMOTE算法的基础上使用差分进化算法自动搜索最优参数,实现性能上的显著提升,被广泛应用于解决相关工作中其他存在的类不平衡问题(如缺陷预测等)。值得注意的是,为了确保模型评估的客观性,本文严格遵循数据划分原则,即仅对训练集进行SMOTUNED过采样处理,而保持测试集数据的原始分布不变。
SMOTE 的核心思想
- 过采样 :针对少数类样本(如关键类),通过线性插值 生成新样本,增加其数量以平衡类别分布。
- 步骤 :
- 对每个少数类样本,找到其 k 个最近邻(k 为人工设定参数)。
- 随机选择一个邻居,按比例生成新样本(例如,在两点之间随机取点)。
2.3.2 随机森林模型
随机森林 (Random Forest) 是一种集成学习模型,由多棵决策树构建,通过将多个弱分类器组合成强分类器。该算法采用Bagging思想,即每次有放回地从训练集中随机抽取样本,利用多棵独立决策树对样本进行训练,并通过投票组合输出分类结果。随机森林有效解决了决策树的过拟合问题,广泛应用于关键类预测和缺陷预测等研究。Osman等人对比了10种机器学习技术,发现随机森林在关键类预测中的表现优于其他模型。需要注意的是,在模型训练过程中,随机森林参数保持默认设置,这是由于本研究旨在比较模型基于度量集的差异,而非评估模型性能的优劣。
3 实验设计
为了评估加权有向网络指标集的有效性,本文设计并展开了充分的实验,旨在解决“WDNM在关键类预测模型上的表现是否优于指标集DM和NM?”的研究问题。
本文将WDNM与DM作为对照组,目的是验证网络度量和软件设计指标在随机森林模型上的表现。另外,WDNM与NM最大的区别在于前者的各项指标是加权有向的,而后者集合中的各项指标在计算类重要性时却忽略了类的依赖强度(权重)。因此,本文将WDNM和NM进行比较,以此验证在加权有向网络指标集上构建的关键类预测模型是否优于无权有向网络指标集上构建的模型。
本文所有实验在Linux系统(5.15.0-124-generic) 32GB内存和2个24GB显存的NVIDIA GeForce RTX 3090 型号GPU上进行。所使用的随机森林模型从sklearn库中导入,参数均使用默认参数。
3.1 实验系统
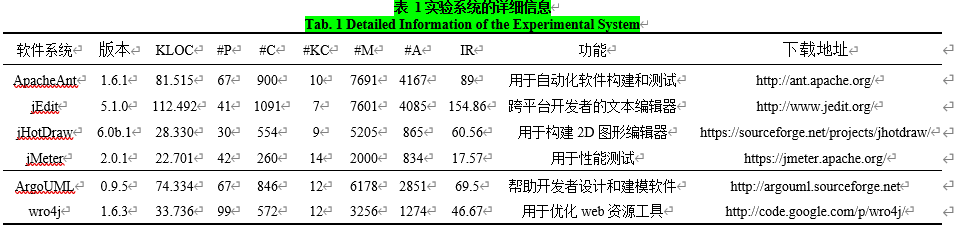
本文选取了在工业界开源且被广泛应用的6款Java软件,这些软件无论是设计模式还是功能均存在异质性,软件的信息如表 1所示。其中,KLOC 列表示表示千行代码数,#P、#C、#KC 、# M和# A列分别表示包的个数、类的总数、关键类的个数、方法的个数和属性的个数, IR列表示每款软件的类不平衡率,即非关键类的数量与关键类的数量的比值。在个别软件中,例如Apache Ant、jEdit等软件,非关键类和关键类的样本量分布不均的情况非常严重。因此对类不平衡问题进行处理就显得尤为必要。
3.2 对比度量集
(1) 软件设计度量(Design Metrics,DM)
Osman等人采用逆向工程技术将Java软件源代码转化为类图。随后,从类图中抽取11项类级软件设计指标,通过将这些指标作为特征输入到有监督分类模型中,用于关键类的预测。由于该指标集是基于软件的设计模式,因此本文将其称为DM。DM包括两种类型的类级度量,分别是规模(Size)和依赖关系 (Coupling) 。DM的详细信息如表 2中DM部分所示。
表2软件设计度量
Tab. 2 Software Design Metrics
| 软件设计度量 | 指标名称 | 所属类别 | 描述 |
| DM | NumAttr | Size | 在一个类中成员变量的数量 |
| NumOps | Size | 类内的方法总数 | |
| NumPubOps | Size | 类内Public方法的数量 | |
| Setters | Size | Setter方法的数量 | |
| Getters | Size | Getter方法的数量 | |
| DepOut | Coupling (Export) | 某个类通过局部变量访问或方法调用等依赖其他类的数量 | |
| DepIn | Coupling (Import) | 某个类被其他类使用(依赖)的数量 | |
| ECAttr | Coupling (Export) | 是指当前类被其他类定义为属性类型的数量 | |
| ICAttr | Coupling (Import) | 某个类的属性其类型是其他类的总数 | |
| ECPar | Coupling (Export) | 是指当前类被其他类定义为参数类型的数量 | |
| ICPar | Coupling (Import) | 一个类内的方法参数类型是其他类的总数 | |
| NM | Barycenter | Network | 网络中某个类的重心中心性值 |
| Betweenness | Network | 网络中某个类的中介中心性值 | |
| Closeness | Network | 网络中某个类的接近中心性值 | |
| Eigenvector | Network | 网络中某个类的特征向量中心性值 | |
| Hub | Network | 网络中某个类的链接权威度(Hub) | |
| Authority | Network | 网络中某个类的内容权威度(Authority) | |
| PageRank | Network | 网络中某个类的PageRank值 |
(2) 无权网络度量集(Network Metrics,NM)
Thung等人提取类图中“泛化”、“实现”和“依赖”等三种类型的依赖关系构造无权有向类级网络,并应用HITS和PageRank等6种算法构造网络度量集。由于这些度量是基于无权有向的软件网络,因此本文将其称为NM。NM的详细信息如表 2中NM部分所示。
3.3评估指标
本文采用AUC指标对关键类预测方法的性能进行评估。AUC (Area Under the Receiver Operating Characteristic Curve) 是一种衡量分类模型优劣的评价指标,由ROC曲线下与坐标轴围成的面积求和得到。ROC曲线如右图图3实线所示。横坐标表示“假正例率”(False Positive Rate,简称FPR),纵坐标表示“真正例率”(True Positive Rate, 简称TPR)。计算公式如下:
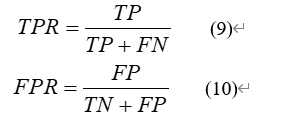
其中,TP为模型正确预测的关键类数量,FN为实际关键类但模型未预测为关键类的数量,FP为实际非关键类但模型错误预测为关键类的数量。ROC曲线上的点则对应于坐标(TPR, FPR)。假定ROC曲线是由坐标为{(x1, y1),…,(xn, yn)}的点按序连接形成。AUC则被估算为:
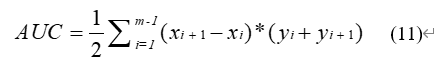
AUC的取值范围为从0到1,越接近1表示模型预测性能越好。本文将AUC作为评估指标的原因有以下两点:首先,AUC指标在同类工作以及其它软件工程任务中被广泛作为模型的评估指标。其次,考虑到本文开展实验的软件系统中存在较为严重的类不平衡问题,而AUC指标对正负样本比例的变化并不敏感,这样能够尽可能地避免由样本不均衡带来的影响,从而更加公平地评估指标集在关键类预测模型上的性能。
3.4 实验结果与分析
本文针对每款软件使用DWM加权机制构造CCNWD。接着,将七种加权有向的网络度量分别应用在CCNWD中,构造网络指标集WDNM,并展开了充分的实证研究。通过将WDNM指标与DM、NM度量指标分别应用于6个开源的软件系统中来评估加权有向网络指标集的有效性。
表 3对应WDNM与其余两种网络度量(DM和NM)分别构建的预测模型性能对比情况。表的左侧详细列出了三种度量集DM、NM和WDNM在6款软件中的AUC结果。针对每款软件最高的AUC值以粗体加以表示。需要注意的是,当使用不同度量集构造关键类预测模型时,可能存在AUC值相差甚微的情况。如表 3所示,在WDNM和NM上构建的模型预测软件wro4j中关键类的AUC结果仅相差0.0012,这种细微差异可能是由于随机森林的随机性引起的。虽然本文通过采用重复交叉验证取平均值的策略试图缓解该问题,但却无法完全避免。为了更加直观地看出各度量集构建的关键类预测模型之间的显著差异,本文采用两两的比较的方式将WDNM、NM和DM两两分为了三组,对于每组均采用非参数检验Wilcoxon来比较各组之间是否存在显著差异。这三组实验分别为1) NM vs. DM;2) WDNM vs.DM;3) WDNM vs. NM。前两组主要用于比较网络度量指标与软件设计指标,最后一组则是用于验证加权有向网络度量对关键类预测模型带来的提升。对于每组测试来说,“>”意味着前者在统计学上大于后者,而“<”则恰好相反。“=”则表明两组实验的结果并没有统计学意义上的差异,即无法拒绝Wilcoxon符号秩检验中的原假设。“**”以及“*”表示显著水平,其中“**” 表示0.01的显著水平,即Wilcoxon符号秩检验p值<0.01,“*”则表示0.05的显著水平,即Wilcoxon符号秩检验p值<0.05。表格中Average行是不同模型在6款软件下的平均AUC值及三组实验性能提升的百分比,最后一行描述了三组实验在统计检验上的Win/Tie/Loss结果。
表3 DWM加权方式下, WDNM vs. DM以及WDNM vs. NM的对比结果
Tab. 3 Comparison results of WDNM vs. DM and WDNM vs. NM in DWM weighting approach
| System | DM | NM | WDNM | NM vs. DM | WDNM vs.DM | WDNM vs. NM |
| Apache Ant | 0.7734 | 0.5587 | 0.8267 | = | = | >,* |
| jEdit | 0.6086 | 0.6110 | 0.5488 | = | = | = |
| jHotDraw | 0.7159 | 0.6505 | 0.8334 | = | = | >,** |
| jMeter | 0.6861 | 0.8183 | 0.7734 | >,** | >,* | = |
| Argo UML | 0.8329 | 0.7775 | 0.9121 | = | >,** | >,** |
| wro4j | 0.9361 | 0.9431 | 0.9443 | = | = | = |
| Average | 0.7588 | 0.7265 | 0.8065 | −4.26% | +6.29% | +11.00% |
| Win/Tie/Loss | 1/5/0 | 3/3/0 | 3/3/0 |
首先对于第一组实验NM vs. DM,通过表 3可以观察到NM仅在JMeter软件中具有突出的表现(Win=1),在5款软件中难以比较两类指标构建的模型预测关键类的性能优劣(Tie=5),通过计算6款软件的平均AUC可以看出NM对DM的下降约为4.26% (-4.26%)。
接着分析第二组实验WDNM vs. DM,可以清楚观察到对比DM,WDNM在3款软件中有较为显著的提升(Win=3)。在其余的3款软件中并没有体现出明显的差异 (Tie=3),虽然在个别软件例如jEdit可能AUC略低,但在统计学上认为这种差异并不显著(即Wilcoxon 检验结果为“=”)。与此同时,WDNM没有在任何一款软件的表现明显差于DM (Loss=0)。6款软件的AUC平均值显示WDNM对DM具有较为明显的提升(+6.29%)。这两组对照实验说明网络度量指标在关键类预测问题上的表现优于软件设计度量指标。
最后,对于第三组实验WDNM vs. NM,可以观察到WDNM在6款软件中的3款软件具有突出的表现 (Win=3),在3款软件中难以比较两类指标构建的模型预测关键类的性能优劣(Tie=3)。与此同时,WDNM没有在任何一款软件的表现明显差于NM (Loss=0)。通过比较6款软件中的平均AUC值可以发现WDNM在整体上优于NMs,平均AUC提高了11.0%。通过这项对照组说明了相比较于Thung等人提出的无权有向网络度量,在加权有向的网络度量集上构建的模型展示出更优异的关键类预测性能。由此可见,在构造软件网络时进一步考虑软件内部的类依赖强度,能够在一定程度上改进关键类预测模型的性能。
4 结论
本文利用静态分析技术从软件源代码构建软件的加权有向网络模型CCNWD,进而构建面向加权有向网络的指标集WDNM。最后,将获取的指标集作为特征经SMOTUNED算法进行类不平衡处理后输入到随机森林模型中,以实现关键类预测。
数据实验表明:
1) 相较于现有的无权有向网络指标集NM,以WDNM为特征构建的关键类预测模型性能(AUC)提高了6%以上;
2) 通过将DM+WDNM作为特征构建关键类预测模型,使得已有的预测模型性能(AUC)提高了11%;
3) 相较于在传统的软件设计度量特征的基础上结合网络度量指标,以此构建的关键类预测模型性能(AUC)平均提高了8%以上。






Comments NOTHING