第一章
统计学:是收集、处理、分析、解释数据并从数据中得出结论的科学。
描述统计:研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。
推断统计:是研究如何利用样本数据来推断总体特征的统计方法。
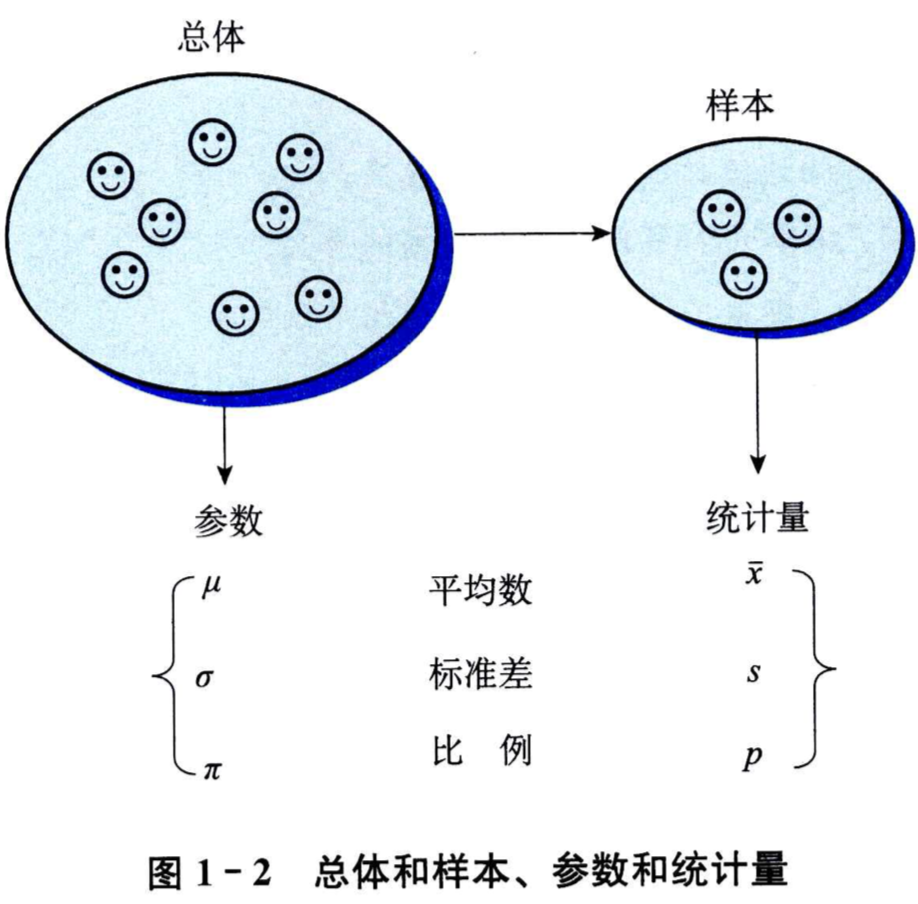
总体:是包含所研究的全部个体(或数据)的集合,它通常由所研究的一些个体组成。
个体:组成总体的每个元素称为个体。
有限总体和无限总体:为了判别在抽样中每次抽取是否独立,将总体分为了有限总体和无限总体
样本:是从总体中抽取的一部分元素的集合,构成样本的元素的数目称为样本量。
样品构成了样本
参数:是用来描述总体特征的概括性数字度量,它是研究者想要了的总体的某种特征值。
统计量:是用来描述样本特征的概括性数字度量。
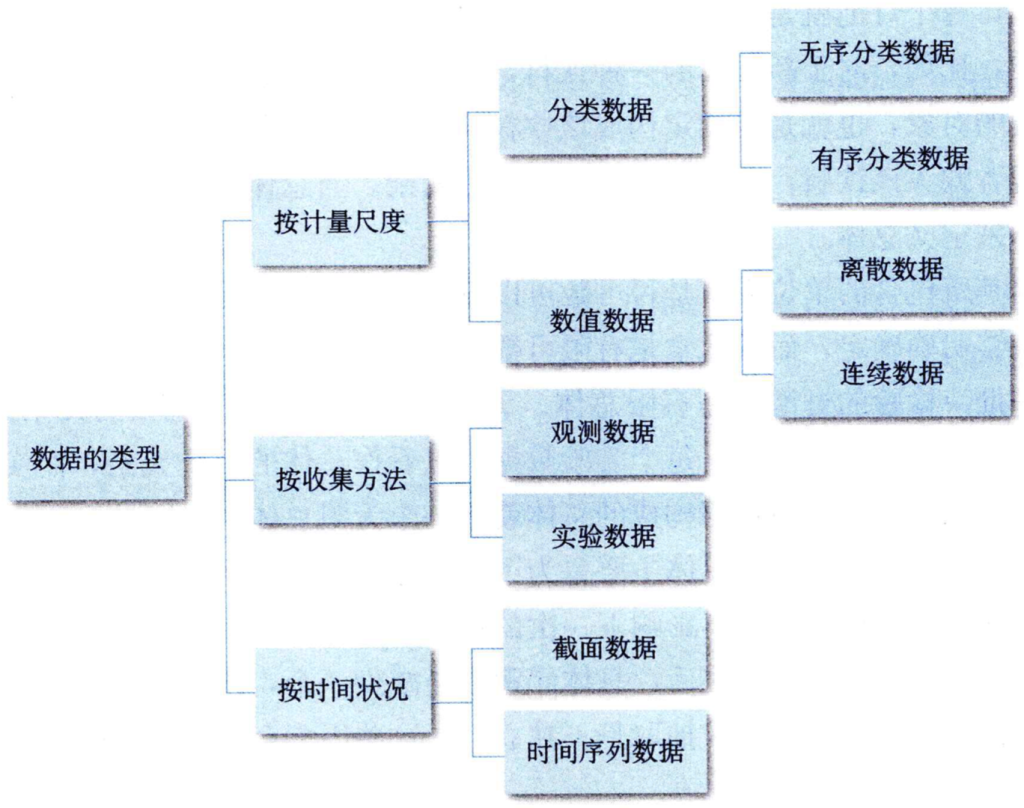
变量:是说明现象某种特征的概念,其特点是从一次观察到下一次观察结果会呈现出差样或变化。
基本类型有:分类变量和数值变量
分类变量:根据有序和无序分为无序分类变量和有序分类变量两种。
数据变量:是取值于数字的变量,也称为定量变量。根据其取值的不同,可以分为离散变量和连续变量。
离散变量是只能取有限个值的变量;连续变量是可以在一个或多个区间中取任何值的变量,它的取值是连续不断的。
第二章
初始调查:
- 观测数据
- 实验数据
使用者:
- 直接来源 —— 一手数据
- 间接来源 —— 二手数据
二手数据的评估与特点:
二手数据:原信息已经存在,对其重新加工、整理,间接来源的数据可以取自系统外部,也可以取自系统内部。
特点:
- 搜集比较容易,采集数据的成本低,并且能很快得到。
- 作用也非常广泛,提供研究问题的背景,研究问题的思路和途径。
- 研究中优先考虑二手数据。
注意事项:使用二手数据时,应注明数据的来源。
组织形式:
- 普查
- 抽样调查
- 概率抽样调查
- 非概率抽样调查
概率抽样:也称随机抽样,是指遵循随机原则进行的抽样,总体中每个单位都有一定的机会被选入样本。
随机不等于随便。
概率抽样的方法:
- 简单随机抽样:有完整的抽样框,又称“抽签法”。优点:比较方便。缺点:估计的精度不够高。
- 分层抽样:层和层之间差异要大。 优点:包含有各种特征的抽样单位。
- 整群抽样:群和群之间差异要小。优点:大大减少了编制抽样框的工作量。缺点:估计的精度较差。
- 多阶段抽样:二阶段抽样,群为初级单位。优点:保证的样本相对集中,从而节省了调查费用。
统计分析的样本主要是概率样本,即样本是采用概率抽样方法得到的。
非概率抽样的方法:
- 方便抽样:样本单位的确定带有随机性
- 判断抽样:优点:抽取样本成本比较低,也容易操作。缺点:是主观的,不能用于对总体的有关参数进行估计。
- 自愿样本:与抽样的随机性无关,样本的组成往往集中于某类特定的人群。
- 滚雪球抽样:用于对稀少群体的调查
- 赔额抽样:按一定的标志分为若干类,然后每类中采用方便抽样或判断抽样的方式选取样本单位。
交叉变量控制可以保证样本的分布更为均匀,但现场调查中为了保证配额的实现,操作难度可能要大一些。
概率抽样和非概率抽样的区别
| 类别 | 概率抽样 | 非概率抽样 |
| 样本分布 | 理论分布存在 | 不确切 |
| 精度 | 有要求 | 没有要求 |
| 特点 | 研究对象总体的数量特征,对精度提出要求 | 操作简便、时效快、成本低 |
搜集数据的基本方法:
- 自填式
- 面访式
- 电话式
- 观察式
数据搜集方法的选择:
- 抽样框中的有关信息
- 目标总体的特征
- 调查问题的内容
- 有形辅助的使用
- 实施调查的资源
- 管理与控制
- 质量要求
实验组和对照组:其产生遵循随机原则。
实验设计本身就是一个统计问题,要确定实验所需单位的个数。
抽样误差:是由抽样的随机性引起的样本结果与总体真值之间的差异,描述的是所有样本可能的结果与总体真值之间的平均差异。
抽样误差大小的因素:样本的大小、总体的变异性。
非抽样误差:是指除抽样误差之外的,由其他原因引起的样本观测结果与总体真值之间的差异。
非抽样误差因素:
- 抽样框误差
- 回答误差
- 无回答误差
- 调查员误差
- 测量误差
第三章
数据的预处理包括:数据审核、数据筛选、数据排序。
数据审核注重审核数据的适用性和时效性。
频数:是落在某一特定类别或组中的数据个数。
分类数据的整理表有:
- 频数分布表(简单频数表)
- 列联表
- 条形图
- 帕累托图
- 饼图
- 环形图
数据分组:是根据统计研究的需要,将数据按照某种标准分成不同的组别,分组后的数据称为分组数据,一个组中最小值称为下限值,一个组中最大值称为上限值。
数值数据分组方法:单变量分组、组距式分组。
组距式分组的步骤/对数值型数据进行数据分组的步骤:
- 确定组数,不少于5组且不多于15组,即5<=k<=15。
- 确定各组的组距,组距=(最大值-最小值)/组数
- 根据分组制作频数分布表
组中值:是每一组中下限值与上限值中间的值,即组中值=(下限值+上限值)/2
直方图:矩形的宽度是组距,高度是频数。
直方图和条形图的区别:
- 条形图是用条形的长度表示各类别频数的多少,其宽度则是固定的
- 直方图是用面积表示各组频数的多少,矩形的高度表示每一组的频数或百分比,宽度则表示各组的组距,其高度与宽度均有意义
- 直方图的各矩形通常是连续排列,条形图则是分开排列
- 条形图主要用于分类数据,直方图为数值型数据
箱形图看课本P48-49页
散点图、雷达图
第四章
数据分布特征的描述:
- 分布的集中趋势
- 分布的离散程度
- 分布的形状
集中趋势是指一组数据向某一中心考虑的程度,它反映了一组数据中心点的位置,统计量主要有平均数、中位数、四分位数。
平均数在参数估计和假设检验中经常用到。
下开口的组中值=相邻组的组中值-相邻组的组距
上开口的组中值=相邻组的组中值+相邻组的组距
众数、中位数和平均数的比较:
- 众数是一组数据分布的峰值,其缺点是不具有唯一性。只有在数据量较大时才有意义。适合作为分类数据的集中趋势测度值。
- 中位数是一组数据中间位置上的值,不受数据极端值的影响。当一组数据的分布偏斜程度较大时有意义。适合作为顺序数据的集中趋势测度值。
- 平均值是针对数值数据计算的,而且利用了全部数据信息,是应用最广泛的集中趋势测度值。当数据呈对称分布或接近对称分布时有意义。缺点是易受数据极端值的影响。







Comments NOTHING